2025年全国高等教育自学考试《线性代数》考前模拟卷

一、单项选择题（本大题共5小题，每小题2分，共10分）

3.设A为4×5矩阵且r(A)=4，则齐次线性方程组Ax=0的基础解系中所含向量的个数为(  )。

A.1

B.2

C.3

D.4

4.设A的特征值为1，-1，向量ɑ是属于1的特征向量，β是属于-1的特征向量，则下列论断正确的是(  )。 

A.ɑ和β线性无关 

B.ɑ+β是A特征向量 

C.ɑ和β线性相关 

D.ɑ与β必正交 

5.下列命题中错误的是(  )。

A.只含有一个零向量的向益组线性相关

B.由3个2维向量组成的向量组线性相关

C.由一个非零向量组成的向量组线性相关

D.两个成比例的向量组成的向量组线性相关

二、填空题（本大题共10小题，每小题2分，共20分）

6.设A，B 都为n 阶对称矩阵，则AB也为对称矩阵的充要条件为       。

7.设A为实对称矩阵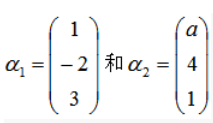，是A属于不同特征值λ1和λ2的特征向量，则a=       。 

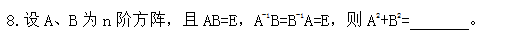
9.设向量=(1，2，3，4)，则的单位化向量为       。

三、计算题（本大题共7小题，每小题9分，共63分）

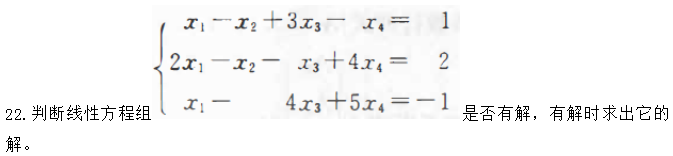
四、证明题（本题7分）

2024年全国高等教育自学考试《线性代数》考前模拟卷

参考答案

一、单项选择题

1.【答案】C

【解析】由代数余子式的定义知，Aij=(-1)i+jMij。

2.【答案】C

【解析】存在可逆矩阵P使B=P-1AP，因此B2=P-1AP・P-1AP=P-1A2P=P-1P=E。 

3.【答案】A

4.【答案】A

【解析】属于不同特征值的特征向量必线性无关。

5.【答案】C

二、填空题

6.【答案】AB=BA

【解析】A，B为n阶对称矩阵，则AT=A，BT=B，因为AB也是对称矩阵。(AB)T=BTAT=BA=AB，故A、B都为n阶对称矩阵，则AB也为对称矩阵的充要条件为AB=BA。

7.【答案】5 

【解析】由于实对称矩阵属于不同特征值的特征向量正交，因此（ɑ1，ɑ2）=a-8+3=a-5=0，所以a=5。 

8.【答案】2E 

【解析】A2+B2=ABB-1A+BA-1AB=EE+EE=E+E=2E。

9.【答案】

【解析】单位化即使各元素的平方加起来为1，，所以单位化向量

为。

10.【答案】a≠-2且a≠1

11.【答案】3 

【解析】

，已知r（A）=3， 

故，故c≠3。

12.【答案】-4 

【解析】。

要谨记如下公式：|kA|=knA。 

|AB|=|A||B|，|A-1|=|A|-1。 

13.【答案】n 

【解析】本题考查利用定义求矩阵的秩，就是利用矩阵的行列式是否为零来确定矩阵的秩，因为A≠0，所以至少有一个元素aij≠0；将IAI按第i行展开，有|A|=＞0，故r（A）=n。 

14.【答案】1

【解析】正惯性指数为3， 负惯性指数为2。所以符号差为3-2=1。

15.【答案】12 

【解析】

对增广矩阵作初等行变换，有，因此可见，r(A)=2，如果方程有解，必有r()=2，因此，所以λ=12。 

三、计算题

16.【答案】

17.【答案】解：

从而ɑ1，ɑ2，ɑ3为一个极大线性无关组，且ɑ4=ɑ1+2ɑ2（答案不唯一）。

18.【答案】（1）设矩阵A的特征值为λ，则由A2+2A=0知，λ2+2λ=0，故λ=0或λ=-2，因为r（A）=2，λ=0不可能是二重根，故A=-2是二重根。 

（2）kE3+A的特征值为k+λ，kE3+A为正定矩阵的充要条件是kE3+A有3个大于0的特征值，故当k>2时，k+λ>0，kE3+A必为正定矩阵。

19.【答案】解：已知r(R) =2，r(S)=2，但R不能由S线性表出，S也不能由R线性表出，故R与S不等价。

20.【答案】

求解非齐次线性方程组

据此可知当λ=15时，β=11-5+0。 

21.【答案】解：由于AB=A2-E，又.

所以A可逆，因此B=A-1(A2-E)=A-A-1

22.【答案】

由此得.

所以方程组无解。

四、证明题

23.【答案】（1）由，，，线性相关得

k1≠0，否者，线性相关，与，，线性无关矛盾，从而得能由，线性表出。

（2）反证法，若能由，，线性表出，可得出也能由，线性表出，与，，线性无关矛盾，从而得不能由，，线性表出。