>>>新疆自考助学报名入口<<<

2025年新疆高等教育自学考试《概率论与数理统计》考前模拟卷

一、单项选择题(本大题共10小题，每小题2分，共20分)

1.A,B为随机事件,且P（A）=0.3,则当（）时，一定有P（B）=0.7。

A.A与B互不相容

B.A与B独立

C.A与B对立

D.A不包含B

2.12颗围棋子中有8颗白子,4颗黑子,从中任取3颗，则这3颗中恰有一颗黑子的概率为（）。

A.0.509

B.0.255

C.0.745

D.0.272

3.已知D（X）=4,D（Y）= 25,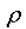XY = 0.6,则D（X-Y）=（）。

A.17

B.19

C.20

D.18

4.设随机变量X服从参数为1/4的指数分布,则E（X）=（）。

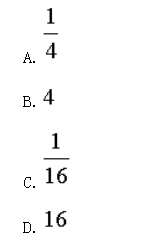
5.极大似然估计（）。 

A.必然是矩估计 

B.是使似然函数取得极大值的点 

C.必然是二阶中心距 

D.必然是无偏估计 

6.随机变量X与Y相互独立且同分布于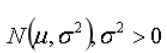，则下面结论不成立的是（）。

A.E(2X-2Y) =0

B.E(2X+2Y) =  

C.D（2X-22Y）=0

D.X与Y不相关

9.A与B相互独立，P(A) >0，P(B) >0，则一定有 P(A U B)=（）。 

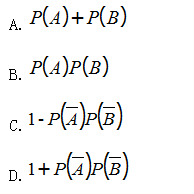
10.从1到100这100个自然数中任取一个，则取到的数能被3整除的概率是（）。

A.0.5

B.0.33

C.0.66

D.0.8

二、填空题(本大题共15小题，每小题2分，共30分)

11.设A1,A2,A3构成一完备事件组,且P（A1）=0.5,P(A2)=0.7,则P(A3) =      。

14.若随机变量 X 满足 E（X）=2，D（X）=4，则 E（X2）=_______。 

15.设E（X）=1,E（Y）=6,E（XY)=7,则Cov(X,Y)=______。

16.设电站供电网有10000盏灯,夜晚每一盏灯开灯的概率都是0.5,而假定所有灯开或关是相互独立的，则夜晚同时开关的灯数在4800-5200的概率为     。

20.若X的分布律为，则E（X2）=______。

21.若E（X）=25，E（Y）=5，则E（5X-25Y）=______。

22.若X与Y独立，E（X）=E（Y）=0,D（X）=D（Y）=1，则E[（X+2Y）2]=_____ 。

23.A与B互不相容，P（A）>0，则P（B|A）=______。

24.若随机变量X的可能取值为1与a，且P{X =1} = 0. 4，E（X）=0.2，则a=_______。

25.甲、乙两人独立地破译一份密码，若他们各人译出的概率均为0.25，则这份密码能破译出的概率为______。

三、计算题（本大题共2小题，每小题8分，共16分）

27.某厂甲,乙两台机床生产同一型号产品,产量分别占总产量的40% ,60%,并且各自产品中

的次品率分别为1%,2%。

求:（1）从该产品中任取一件是次品的概率；

（2）在取出一件是次品的条件下,它是由乙机床生产的概率。

四、综合题（本大题共2小题，每小题12分，共24分）

28设随机变量X服从[0,1]上的均匀分布,Y服从参数为5的指数分布，且X与Y独立。

求：（1）二维随机变量（X,Y）的概率密度;

（2）

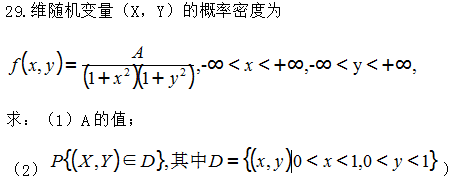
五、应用题（10分）

30.某单位内部有1000台电话,每个分机有5%的时间使用外线通话，假定每个分机是否使用外线是相互独立的,该单位总机至少应安装多少条外线，才能以95%以上的概率保证每个分机需用外线时不被占用?(附:Φ(1.65)= 0. 9505)

2024年湖南省高等教育自学考试《概率论与数理统计》考前模拟卷参考答案

一、单项选择题

1.【答案】C

2.【答案】A

3.【答案】A

4.【答案】B

5.【答案】B

6.【答案】C

7.【答案】C

8.【答案】C

9.【答案】C

10.【答案】B

二、填空题

11.【答案】0.2

12.【答案】0.25 

13.【答案】2

14.【答案】8 

15.【答案】1

16.【答案】0.9375

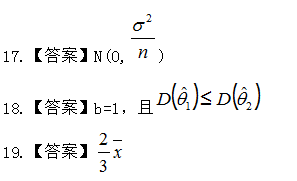
20.【答案】0. 7

21.【答案】0

22.【答案】5

23.【答案】0

三、计算题

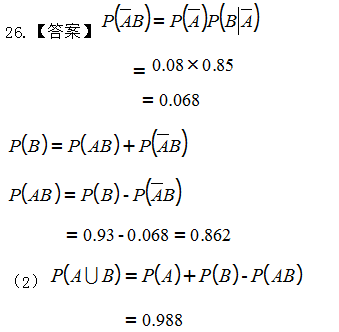
四、综合题

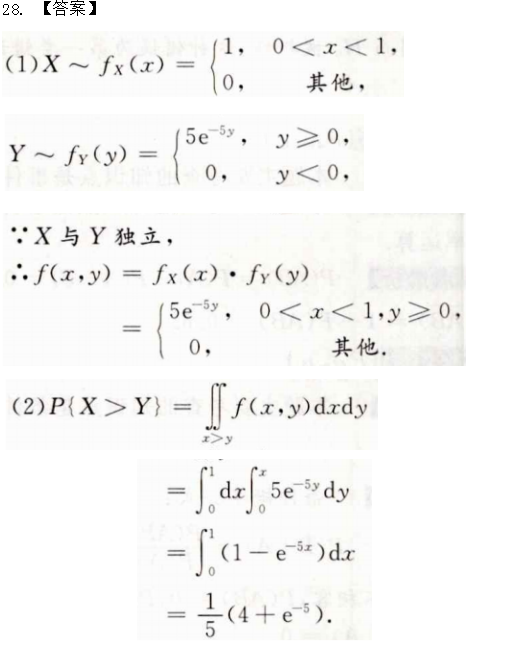
五、应用题

点击咨询老师：2025年新疆自考报名时间、报考流程、报名条件、考试安排、专业介绍、院校选择、自考费用......