全国2005年7月高等教育自学考试《高等数学(工本)》试题
《自考视频课程》名师讲解,轻松易懂,助您轻松上岸!低至199元/科!
本试卷总分100分,考试时间150分钟。
一、单项选择题(每小题2分,共40分)
1.不在-2的2邻区内的点是( )
A.-3
B.-1
C.-1/2
D.0
3.已知当x→0时,e^x-(ax^2+bx+1)是比x^2高阶的无穷小量,则常数a, b满足( )
A.a=1, b=1
B.a=-1, b=-1
C.a=1/2, b=1
D.a=-1/2, b=-1
6.设函数y=y(x)是由方程xy^2-y+1=0所确定的,则![]() =( )
=( )
A.-1
B.0
C.1
D.2
9.设函数F(x)=![]() ,则F′(x)=( )
,则F′(x)=( )
A.
B.
C.
D.
11.设函数f(x)在区间[-3,-1]上连续且平均值为6,则![]() ( )
( )
A.1/2
B.2
C.12
D.18
12.点(0,1,2)到平面x-2y+2z-6=0的距离为( )
A.4/3
B.0
C.2/3
D.4
14.若函数f(x,y)在(x0, y0)的某邻域内有定义,并且![]() 存在,则f(x,y)在(x0,y0)处 ( )
存在,则f(x,y)在(x0,y0)处 ( )
A.连续
B.不一定连续
C.可微
D.间断
17.在下列函数组中,线性无关的是( )
A.
B.
C.
D.
19.无穷级数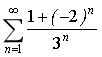 ( )
( )
A.绝对收敛
B.条件收敛
C.发散
D.敛散性不确定
20.幂级数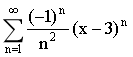 的收敛区间为( )
的收敛区间为( )
A.(2,4)
B.[2,4]
C.(2,4]
D.[2,4)
5.设函数f(x)=|x|,则f′(0)( )
A.等于0
B.等于1
C.等于-1
D.不存在
8.设![]() ,则f(x)=( )
,则f(x)=( )
A.
B.
C.
D.
13.设有直线L:![]() 及平面P:2x-3y+z-6=0,则直线L( )
及平面P:2x-3y+z-6=0,则直线L( )
A.在平面P内
B.与平面P垂直
C.与平面P平行,但不在平面P内
D.与平面P相交,但不垂直于平面P
2.极限![]() ( )
( )
A.0
B.1
C.1/2
D.∞
16.已知区域G是由坐标面和平面x+2y+z=1所围成,则三重积分![]() ( )
( )
A.
B.
C.
D.
4.曲线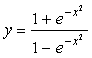 ( )
( )
A.没有渐近线
B.仅有水平渐近线
C.仅有垂直渐近线
D.既有水平渐近线又有垂直渐近线
15.设函数u=x^(yz),则du|(1,1,1)=( )
A.dx
B.dx+dy+dz
C.-dx+dy+dz
D.dy+dz
10.下列广义积分中收敛的是( )
A.
B.
C.
D.
18.微分方程y″+y=0的解是( )
A.y=1
B.y=x
C.y=sinx
D.y=e^x
7.已知函数f(x)在x0的某邻区内二阶可导,并且f′(x0)=0,f″(x0)<0,则( )
A.(x0,f(x0))是函数f(x)的极值点
B.(x0,f(x0))是曲线y=f(x)的拐点
C.x0是函数f(x)的极小值点
D.f(x0)是函数f(x)的极大值
二、填空题(每小题2分,共20分)
1.函数![]() 的反函数为_______________.
的反函数为_______________.
6.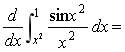 _______________.
_______________.
2.极限![]() =_______________.
=_______________.
9.幂级数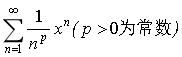 的收敛半径是_______________.
的收敛半径是_______________.
3.曲线y=e^(-x)的水平渐近线是_______________.
10.函数f(x)=![]() 的x的幂级数展开式为_______________.
的x的幂级数展开式为_______________.
4.设函数f(x)=(x-1)(x-2)…(x-100),则f′(1)= _______________.
5.不定积分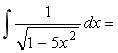 _______________.
_______________.
7.在空间直角坐标系中,点(1,-2,3)关于yoz坐标面的对称点为_______________.
8.设函数z=3^xcos3y,则dz=_______________.
三、计算题(每小题5分,共25分)
1.求极限![]()
3.设函数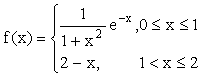 ,求定积分
,求定积分![]() .
.
2.求曲线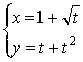 在点P(2,2)处的切线方程。
在点P(2,2)处的切线方程。
4.计算曲线积分![]() 其中C是由A(1,1)到B(2,2)的直线段.
其中C是由A(1,1)到B(2,2)的直线段.
5.求微分方程![]() 的通解.
的通解.
四、应用和证明题(每小题5分,共15分)
1.在椭圆 内作内接矩形,试问其长、宽各为多少时,矩形面积最大?此时面积值等于多少?
内作内接矩形,试问其长、宽各为多少时,矩形面积最大?此时面积值等于多少?
3.已知函数u=f(x+ay)+g(x-ay),其中f和g均为二阶可导函数, 证明: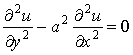 .
.
2.设函数f(x)在(-∞,+∞)内可导,求证:若f(x)为奇函数,则f′(x)为偶函数.
本文标签:新疆自考高等数学(工本)全国2005年7月高等教育自学考试《高等数学(工本)》试题
转载请注明:文章转载自(http://www.xinjiangzikao.com)

《新疆自考网》免责声明:
1、由于各方面情况的调整与变化,本网提供的考试信息仅供参考,考试信息以省考试院及院校官方发布的信息为准。
2、本网信息来源为其他媒体的稿件转载,免费转载出于非商业性学习目的,版权归原作者所有,如有内容与版权问题等请与本站联系。联系邮箱:812379481@qq.com。











